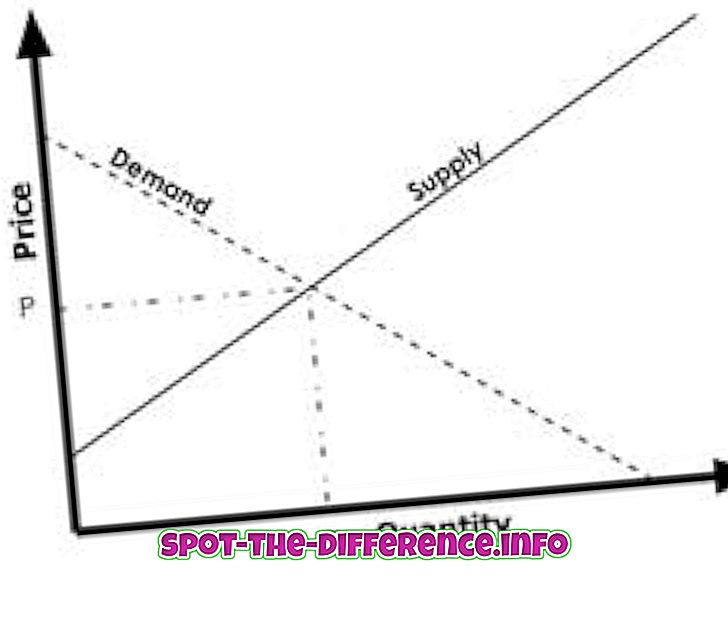
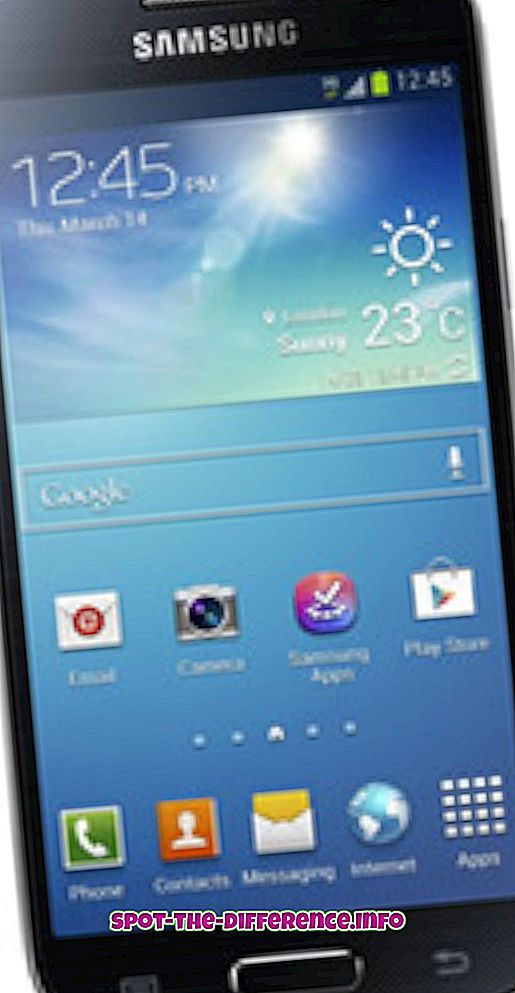
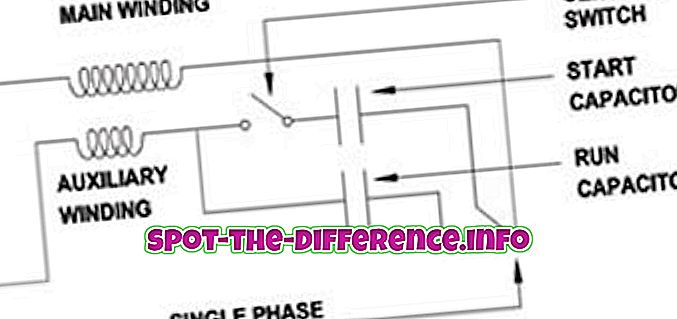
Belangrijkste verschil: een punt is een punt die een locatie aangeeft die is gemarkeerd op een oneindige ruimte of vlak oppervlak. Een lijn wordt als eendimensionaal beschouwd en werd ingevoerd om rechte objecten zonder breedte en diepte weer te geven. Een vlak is een tweedimensionaal plat oppervlak dat oneindig groot is met een dikte van nul.
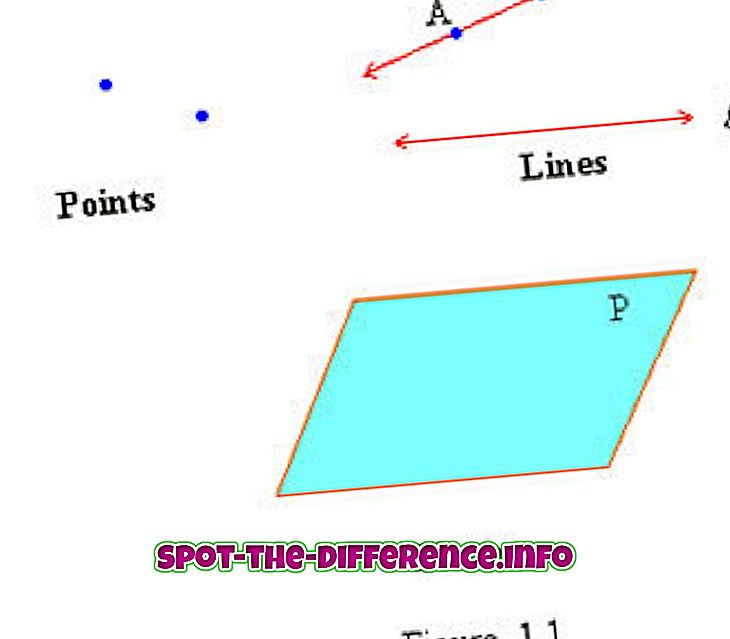
Punt, lijn en vlak worden beschouwd als ongedefinieerde termen van geometrie omdat ze niet formeel zijn gedefinieerd. Wanneer we een term definiëren, gebruiken we meestal eenvoudigere woorden om de term te beschrijven. Een punt, lijn en vlak worden echter beschouwd als al vereenvoudigde termen. Alle andere geometrische concepten zijn gebouwd op het punt, de lijn en het vlak. Laten we echter proberen deze drie niet-gedefinieerde termen te begrijpen.
Een punt is een stip die niets betekent maar in plaats daarvan een positie. Het punt vertegenwoordigt een locatie die is gemarkeerd in de oneindige ruimte of op een vlak oppervlak. Een punt kan een punt van elke grootte zijn, maar het heeft geen lengte, breedte of dikte. Dit komt omdat het een plaats vertegenwoordigt en geen ding.
Punten worden benoemd met een hoofdletter één letter zoals A, B, C, etc. In tweedimensionale Euclidische ruimte, beter bekend als een raster of een grafiek met x-as en y-as, wordt een punt weergegeven door een bestelde paar (x, y). De x staat voor de horizontale plaatsing van het punt, terwijl y staat voor de verticale plaatsing. Er zijn twee sets van punten: collineair en coplanair. De collineaire verzameling van punten ligt in een rechte lijn, terwijl een reeks van co-planaire lijnen op hetzelfde vlak ligt.
Een lijn wordt als eendimensionaal beschouwd en werd ingevoerd om rechte objecten zonder breedte en diepte weer te geven. De definitie van lijn verandert afhankelijk van het type geometrie. In Euclid-geometrie heeft de lijn geen ingestelde definitie. In de analytische meetkunde wordt een lijn in het vlak gedefinieerd als de verzameling punten waarvan de coördinaten voldoen aan een gegeven lineaire vergelijking. In de incidentiemeetkunde kan een lijn een onafhankelijk object zijn van de reeks punten die erop liggen.
Een lijn wordt geaccepteerd als een eendimensionale oneindige set van punten die zijn verbonden. Een rechte lijn is de kortste afstand tussen twee willekeurige punten in een vlak. Lijnen zijn gemarkeerd met twee pijlen aan het einde van elk, om aan te geven dat het nooit eindigt. Lijnen worden op twee manieren benoemd: door twee punten op de lijn of door een enkele kleine letter. Elke twee punten gemarkeerd op een lijn kan worden gebruikt om naar een lijn te verwijzen. Bijvoorbeeld: een regel met punten H, I erop zal worden aangeduid met regel HI en er zal een bovenop worden geplaatst om aan te geven dat het een lijn is.
Een vlak is een tweedimensionaal plat oppervlak dat oneindig groot is met een dikte van nul. Een vlak wordt beschouwd als een tweedimensionaal analoog van een punt (nuldimensies), een lijn (ééndimensionaal) en een effen (driedimensionaal). Bij het beschouwen van de definitie in termen van Euclidische ruimte, verwijst het vlak naar de hele ruimte. Stel je een metalen plaat voor die geen dikte heeft, maar die gaat voor altijd en eeuwig door. Dat wordt beschouwd als een vliegtuig.
Wikipedia stelt: "Veel fundamentele taken in wiskunde, meetkunde, trigonometrie, grafentheorie en grafische weergave worden uitgevoerd in een tweedimensionale ruimte, of met andere woorden, in het vlak." Hoewel vliegtuigen oneindig zijn, hebben ze om te tekenen, nodig randen. Deze vlakken worden getekend door twee parallelle paren en zien eruit als een schuine rechthoek. Het vlak heeft twee dimensies: lengte en breedte. Maar aangezien het vlak oneindig groot is, kunnen de lengte en breedte niet worden gemeten.
Vliegtuigen worden gedefinieerd door drie punten. Er zijn twee soorten vliegtuigen: evenwijdige vlakken en elkaar kruisende vlakken. Parallelle vlakken zijn twee of meer vlakken die oneindig doorgaan zonder elkaars paden te overschrijden. Stel je de oudere metaalplaat voor, voeg nu een nieuwe metaalplaat toe die er bovenop zit en gaat ook voor altijd door. Deze twee zouden twee parallelle vlakken maken die elkaar nooit kruisen. Interessante vliegtuigen zijn echter precies dat. Dit zijn twee vlakken die elkaars pad kruisen. Vliegtuigen worden gewoonlijk genoemd met een hoofdletter met hoofdletters geschreven in cursief (vlak P).
In de geometrie zijn het punt, de lijn en het vlak samengevoegd in de vorm van een postulaat. Dit postulaat is een verzameling van drie aannamen (axioma's) die kunnen worden gebruikt als onderdeel van een basis voor Euclidische geometrie in drie of meer dimensies. De drie veronderstellingen omvatten: Unieke lijnaanname, veronderstelling van aantalregels en veronderstelling van dimensies. De unieke lijnaanname suggereert dat er precies één lijn door twee verschillende punten loopt. De aanname van de nummerregel geeft aan dat elke regel een reeks punten is die in een één-op-één correspondentie met de reële getallen kan worden gezet. Elk punt kan overeenkomen met 0 (nul) en elk ander punt kan overeenkomen met 1 (één). Ten slotte geven de dimensieveronderstellingen een gegeven in een vlak, er bestaat ten minste één punt in het vlak dat niet op de lijn staat. Met een vlak in de ruimte bestaat er ten minste één punt in de ruimte dat niet in het vlak ligt.