Belangrijk verschil: in de wiskunde wordt een vergelijking gebruikt om de gelijkheid tussen twee uitdrukkingen aan te duiden. Een functie daarentegen is veel complexer dan een vergelijking. Een functie wordt gebruikt om een ​​relatie aan te duiden tussen een set ingangen en een set bijbehorende uitgangen.

Een vergelijking en een functie zijn twee van de basisgrondslagen van algebra, een onderwerp in de wiskunde. Beide kunnen vrij complex van aard zijn, maar in hun basisvorm kunnen ze als elkaar verward zijn. Het belangrijkste verschil tussen een vergelijking en een functie is het feit dat een vergelijking meestal een enkele invoer behandelt, terwijl een functie meerdere ingangen kan hebben.

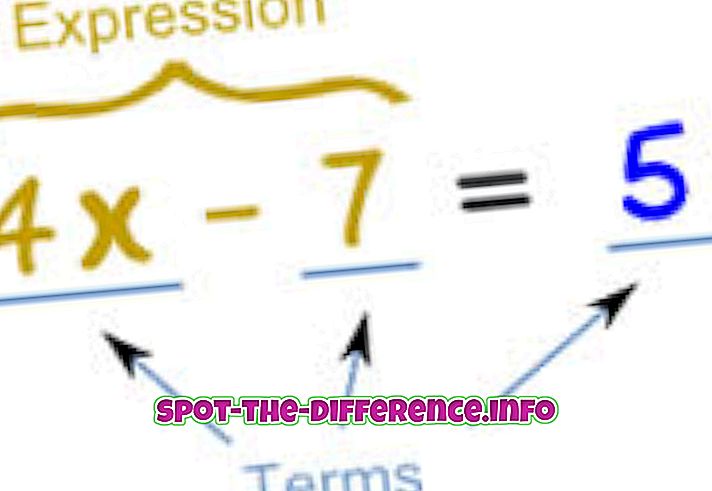
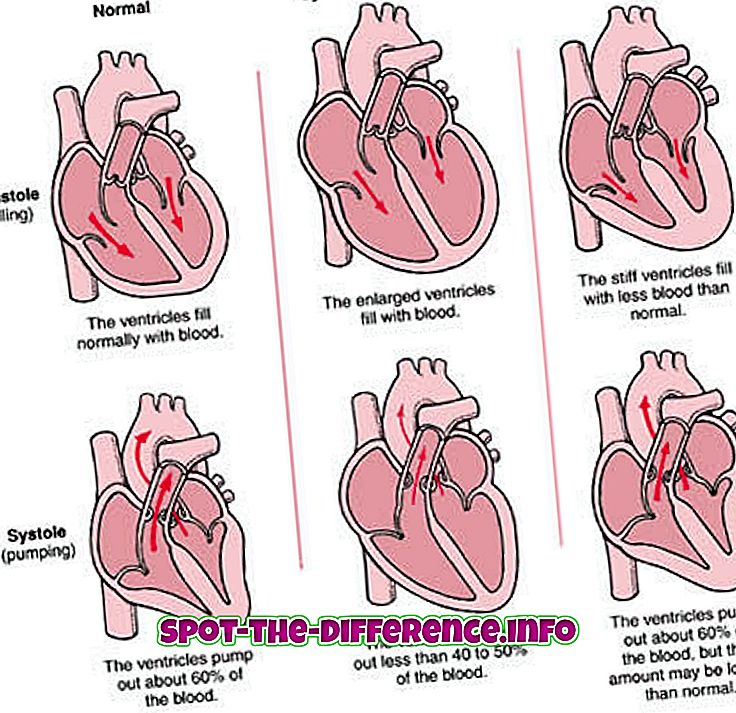
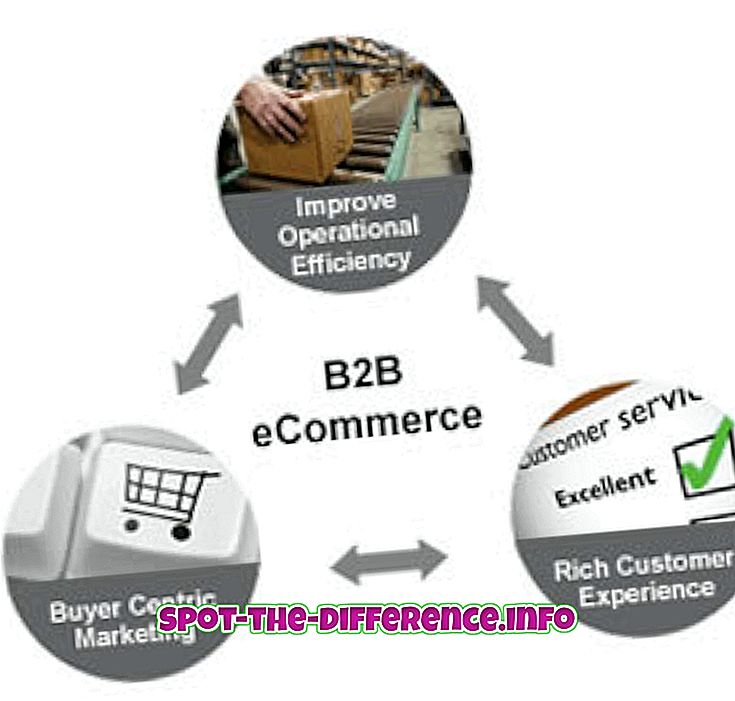
In de wiskunde wordt een vergelijking gebruikt om de gelijkheid tussen twee uitdrukkingen aan te duiden. In wezen wordt een vergelijking geschreven als een uitdrukking die gelijk is aan een andere uitdrukking. Bijvoorbeeld: x + 2 = 5. Dit geeft aan dat wat dan ook x is, als je er 2 aan toevoegt, gelijk is aan 5. Daarom kunnen we de vergelijking voor x oplossen, die 3 is, als 3 + 2 = 5.

Vergelijkingen kunnen complexer zijn dan dat en kunnen meerdere variabelen bevatten, zoals x, y, z, etc. in een enkele vergelijking. Bijvoorbeeld: 3x + 2y - z = 4. Elk alfabet komt echter overeen met één cijfer. In dit geval is x = 1, y = 2 en z = 3.

Vandaar,

3x + 2y - z = 4 wordt

3 (1) + 2 (2) - 3 = 4 wat is

3 + 4 - 3 = 4 in wezen

4 = 4

Een functie daarentegen is veel complexer dan een vergelijking. Een functie wordt gebruikt om een ​​relatie aan te duiden tussen een set ingangen en een set bijbehorende uitgangen. In wezen moet een invoer een enkele uitvoer geven. Een functie is een relatie tussen twee variabelen. Bijvoorbeeld: f (x) = x + 2. Vanaf deze functie, wat dan ook, de invoer is, het geeft je een enkele uitvoer, wat de invoer plus 2 zal zijn. Laten we deze functie oplossen:

Invoer	Functie	uitgang
X	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Enzovoorts…

Functies hebben verschillende toepassingen in wiskunde, natuurkunde, informatica, enz. Ze kunnen variëren van een eenvoudige functie, zoals hierboven aangegeven, tot complexe formules of algoritmen. Een functie kan worden gezien als een machine die een uitvoer voor een invoer levert, en die uitvoer is op de een of andere manier gerelateerd aan de invoer.

Een functie bestaat altijd uit drie delen: de invoer, de relatie en de uitvoer. De klassieke manier om een ​​functie te schrijven is met "f (x) = ...", waarbij x de invoer aangeeft en f (x) de uitvoer aangeeft.

Zoals hierboven vermeld, is het belangrijkste verschil tussen een vergelijking en een functie dat een vergelijking meestal slechts één invoer heeft die ertoe leidt dat de uitdrukkingen gelijk zijn. Terwijl, een functie verschillende ingangen heeft, die elk een uitgang zullen geven.